Joint Spectral Embeddings
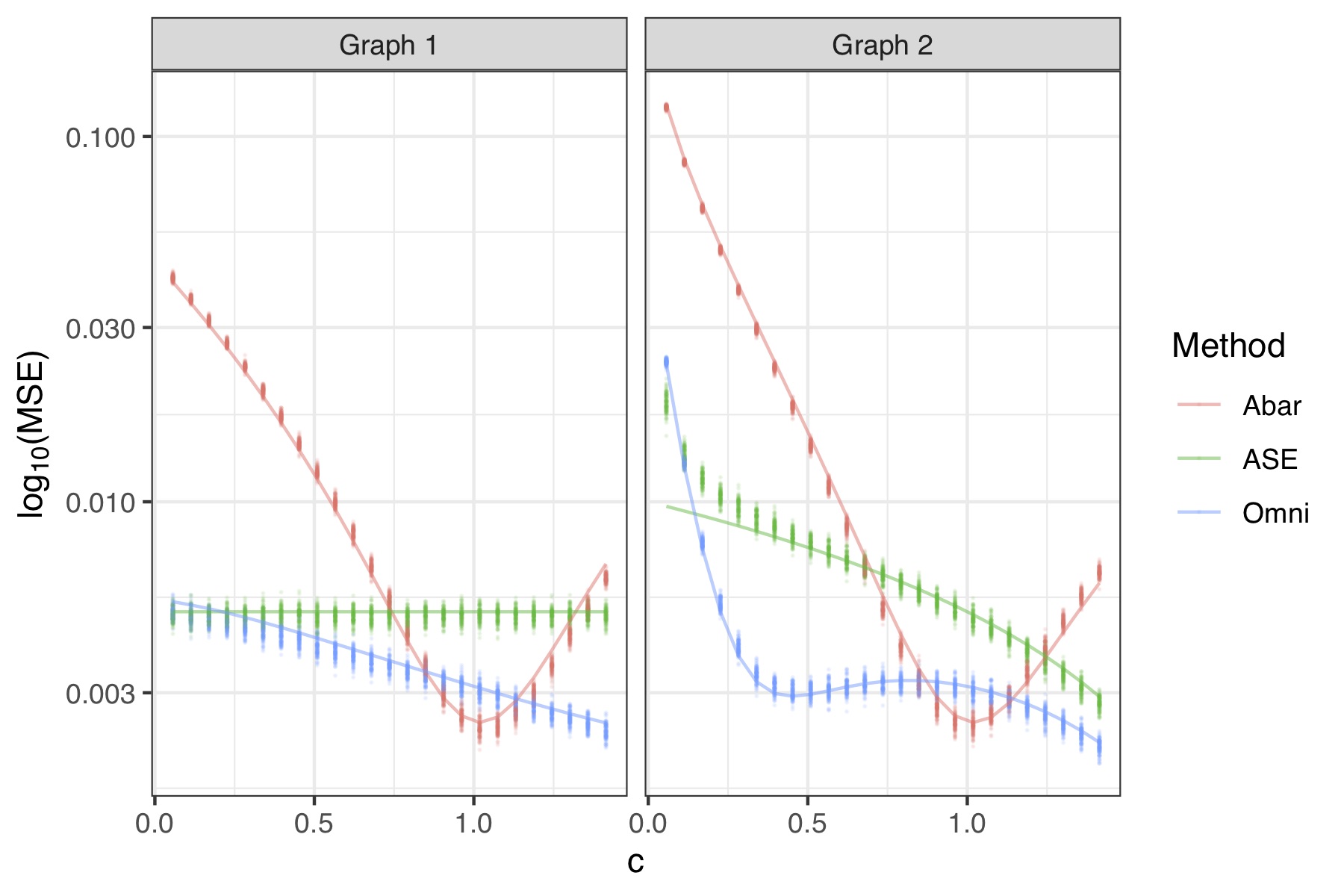
(Preprint. Repository.) Latent position models and their corresponding estimation procedures offer a statistically principled paradigm for multiple network inference by translating multiple network analysis problems to familiar tasks in multivariate statistics. Latent position estimation is a fundamental task in this framework yet most work focus only on unbiased estimation procedures. We consider the ramifications of utilizing biased latent position estimates in subsequent statistical analysis in exchange for sizable variance reductions in finite networks. We establish an explicit bias-variance tradeoff for latent position estimates produced by the omnibus embedding of Levin et al. (2017) in the presence of heterogeneous network data. We reveal an analytic bias expression, derive a uniform concentration bound on the residual term, and prove a central limit theorem characterizing the distributional properties of these estimates. These explicit bias and variance expressions enable us to show that the omnibus embedding estimates are often preferable to comparable estimators with respect to mean square error, state sufficient conditions for exact recovery in community detection tasks, and develop a test statistic to determine whether two graphs share the same set of latent positions. These results are demonstrated in several experimental settings where community detection algorithms and hypothesis testing procedures utilizing the biased latent position estimates are competitive, and oftentimes preferable, to unbiased latent position estimates.
I have had the opportunity to present this work at the following conferences and workshops.
- Joint Statistical Meetings 2020 - Slides, Presentation
- Joint Statistical Meetings 2019 - Slides
- Center for Information & Systems Engineering Student Workshop - Slides
Sparse Covariance Estimation
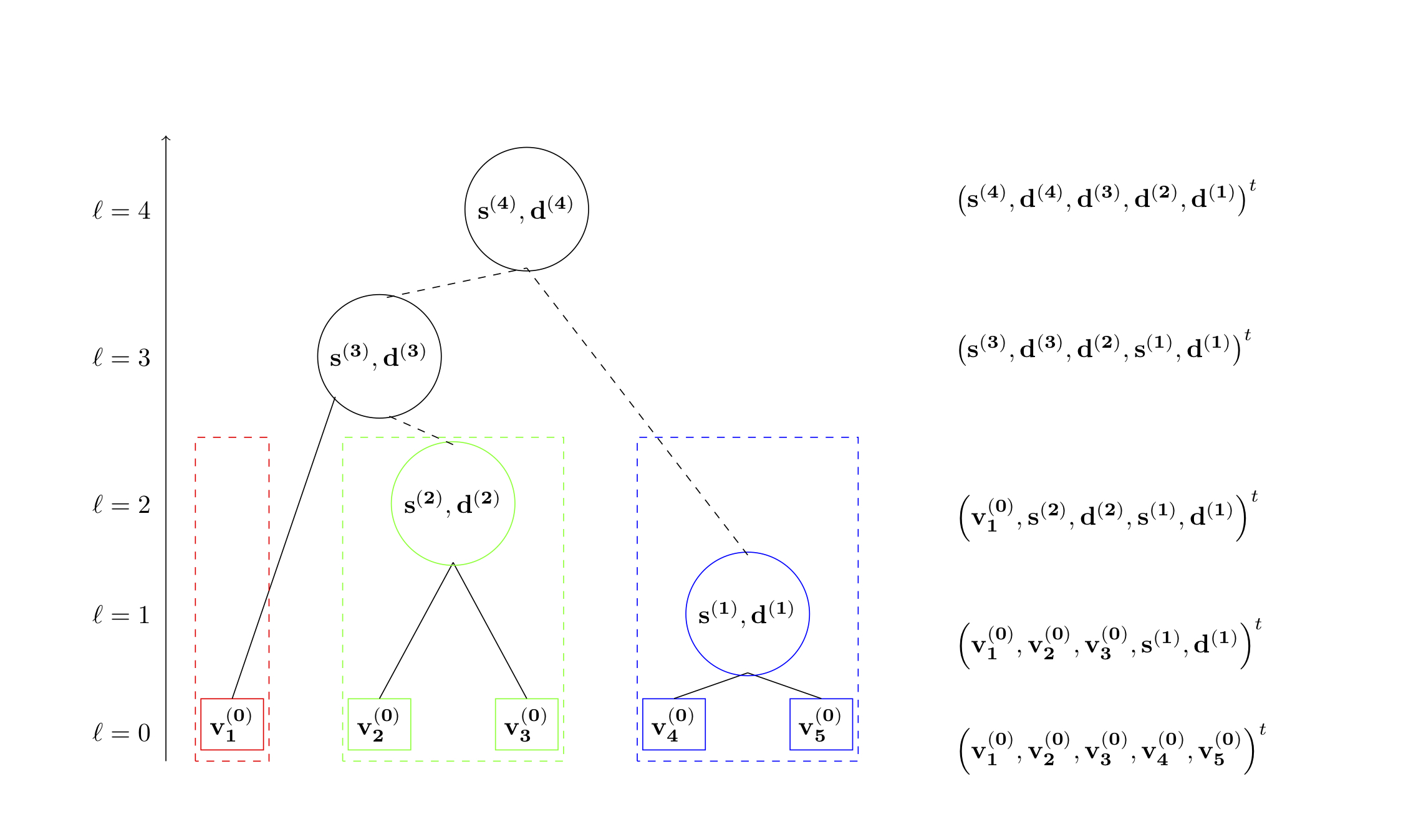
This project focuses on improving the estimates of large, sparse covariance matrices. In several applications, practitioners believe that the correlation between their samples should be relatively low. In practice, however, it is common that samples may be clustered into small homogeneous sets throughout the sample. For example, in large medical studies it is quite common that entire families will participate. While across the dataset there is low correlative structure, the dataset still consists of small closely clustered individuals. To leverage this structure, we use Treelets to construct a smoothed estimate of the covariance matrix through iteratively constructing a basis that more naturally captures the variance in the dataset. Once this is done, we smooth the estimate by thresholding the eigenvalues in this new basis to encourage a parsimonious structure. With several applications in statistical genetics, we used Treelet Smoothers to improve the estimate of distant relatedness.
I have had the opportunity to present this work at the following conferences and workshops.
Course Projects
Here is a list of course projects that I have worked on in graduate school.